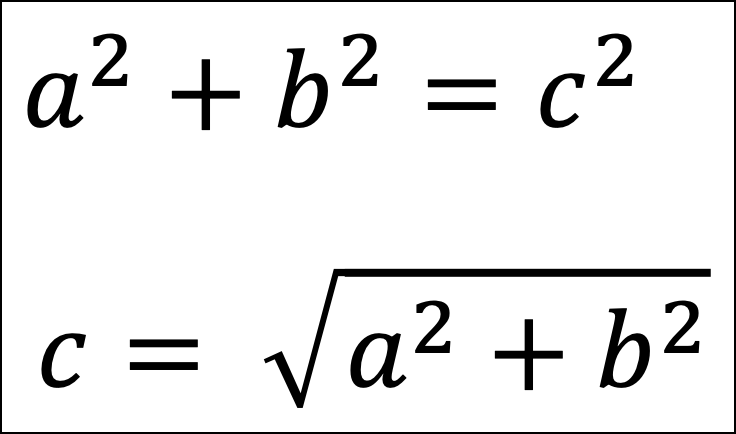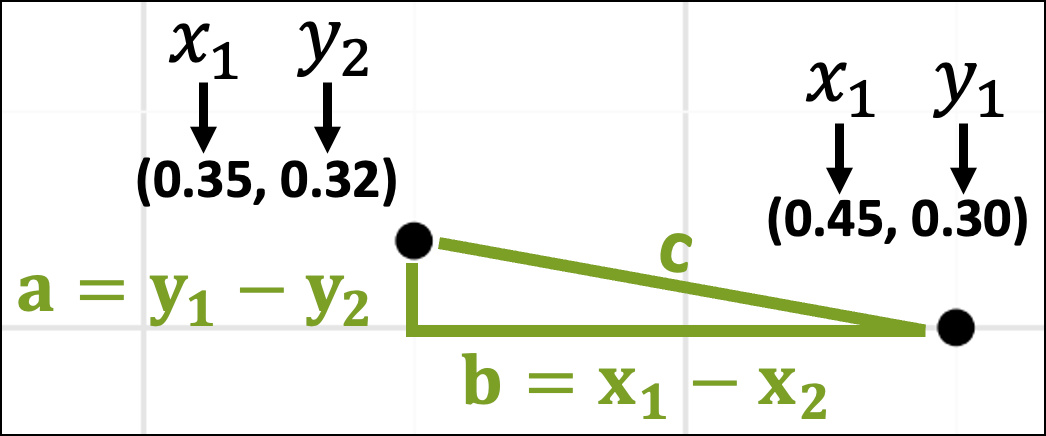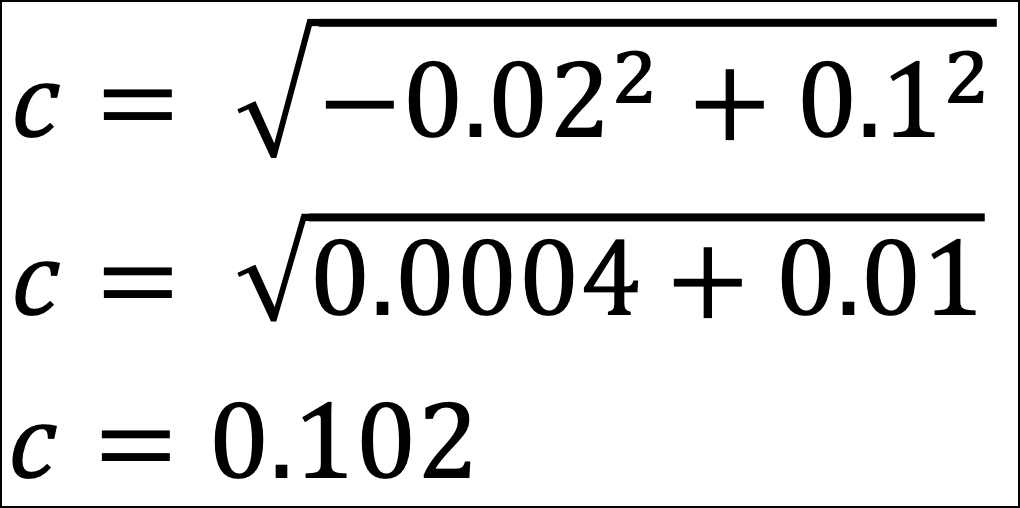Join 7,715 professionals who get data science tutorials, book recommendations, and tips/tricks each Saturday.
New to Python? I'll teach you for free.
I won't send you spam. Unsubscribe at any time.
Issue #16 - Hierarchical Clustering Part 3: Calculating Distance
This Week’s Tutorial
NOTE - I will assume you've read the second tutorial in this series.
Every clustering algorithm that you commonly use in DIY data science needs some way to calculate the distance (i.e., similarity) between two rows of data.
Euclidian distance is the default way to calculate distance in these algorithms.
For example, the two most commonly used clustering algorithms (i.e., k-means and DBSCAN) I teach in my Cluster Analysis with Python online course also use Euclidian distance.
Don't panic! Euclidian distance is a fancy name for something you learned in elementary or middle school - the Pythagorean theorem.
This tutorial will demonstrate how this works using a simple step-by-step graphical approach.
To jog your memory, here's the hypothetical dataset from the last tutorial:
And the scatter plot of the dataset:
As discussed in the last tutorial, the agglomerative hierarchical clustering algorithm calculates distances between all the pairs of data points in the dataset.
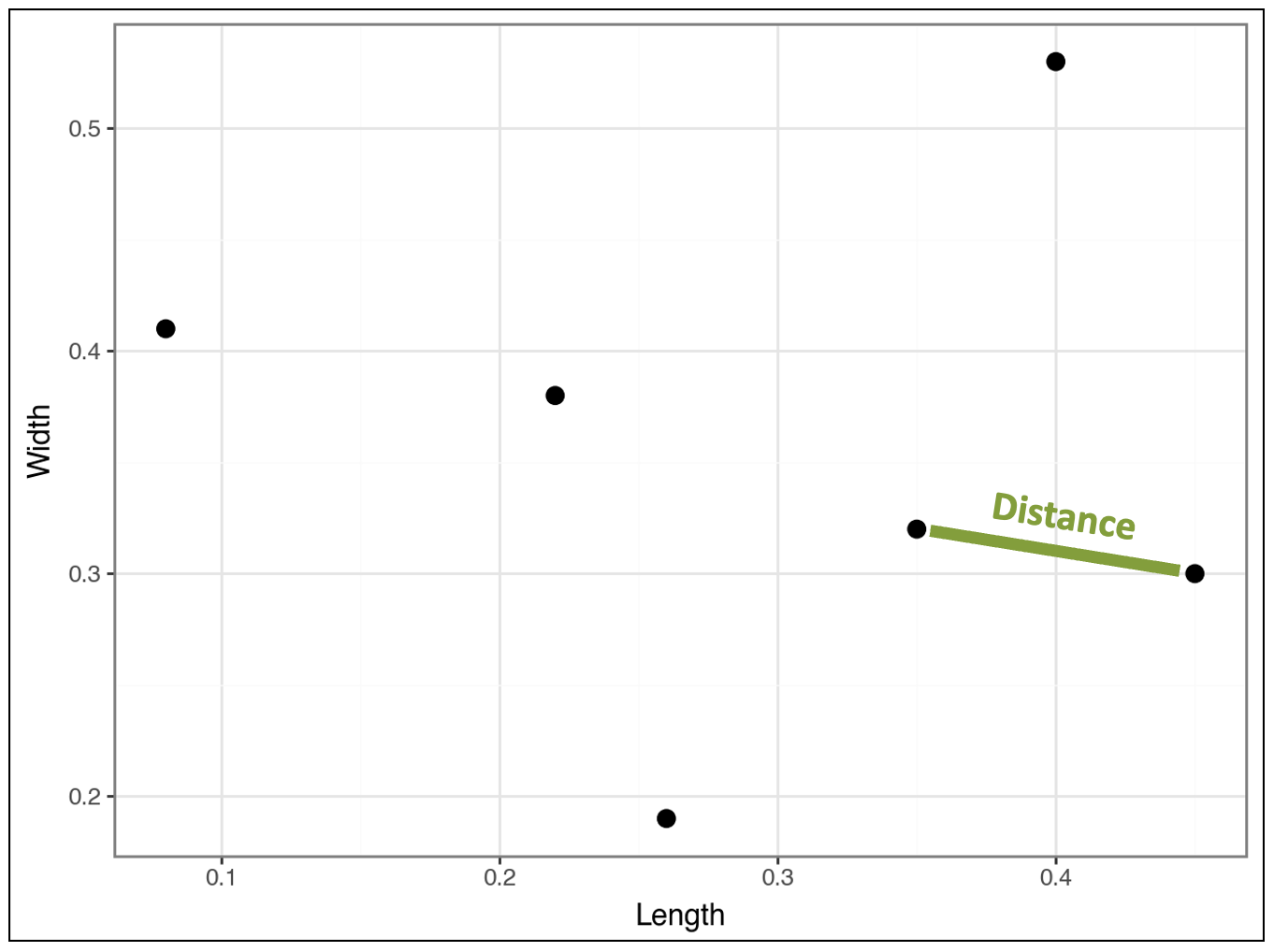
The algorithm finds that the following two data points (i.e., rows) are closest and clusters them:
The tutorial will use these two data points to explain Euclidian distance.
Intuitively, we know the distance between these two data points is represented by the line below:
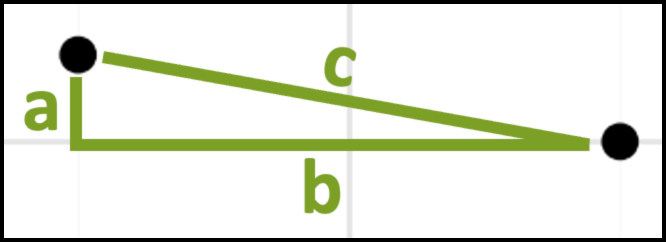
Zooming in on these two data points, we can also imagine them as being part of a triangle with each side of the triangle labeled a, b, and c:
As you might recall from school, the Pythagorean theorem gives the mathematical relationship between the lengths of the sides of the above triangle:
From the above images, we now have a way to calculate the distance between the two data points - it's the length of side c!
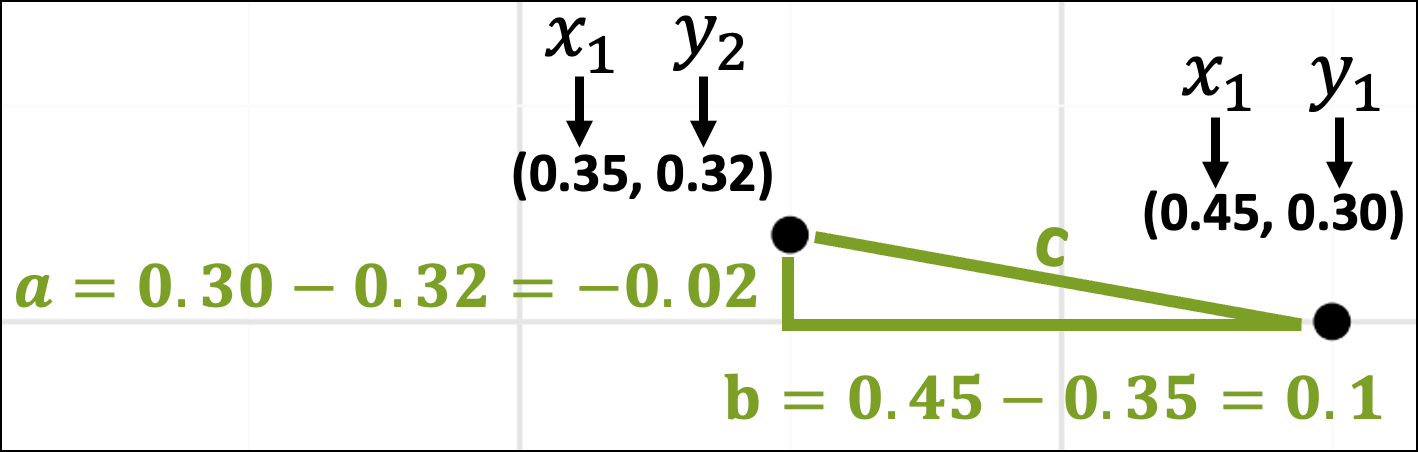
Plugging the data points into the Pythagorean theorem will calculate the distance. To do this, we'll need the data values:
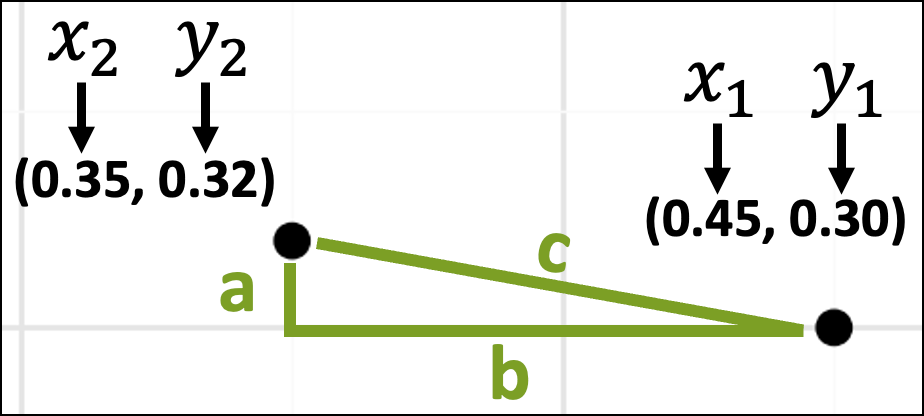
The above image shows which dataset rows correspond with the data points in the scatter plot. The image also displays the data values for each row.
The next step is to think about these data values in terms of the x-axis and y-axis coordinates:
With the coordinates in place, the lengths of the sides of the triangle are just the differences in the x-axis and y-axis coordinates:
The rest is simple plug-and-chug math:
The distance between the Row 2 and Row 5 data points is 0.102.
Now, here's the magic of the Pythagorean theorem.
It's Euclidian distance in two dimensions (e.g., a triangle is a 2D shape). The same ideas behind the Pythagorean theorem scale to more dimensions.
For example, all the visualizations above are 2D. They have an x-axis and a y-axis. Consider a 3D visualization. This adds a z-axis.
As shown above, the calculation uses the differences between the x and y values for the data points. In 3D, this would include a difference for the z values:
The above pattern scales beyond 3D. In other words, if you have 15 columns in your dataset, there would be 15 different terms under the square root symbol.
The good news is that Python will calculate all this for you automagically.
The important part for you is the intuition of what's going on with the distance calculation. This is where the Pythagorean theorem helps build your intuition of how clustering determines similarity.
Now you know how agglomerative hierarchical clustering works behind the scenes.
The algorithm iteratively calculates the Euclidian distance between the data points and/or any clusters to build the taxonomy.
As you might imagine, when your datasets have many columns and rows, your laptop has to do a lot of work performing all the calculations.
The larger your datasets, the longer the algorithm will take to run. However, the time spent increases extremely quickly as you add rows/columns (i.e., there's a nonlinear relationship between dataset size and running time).
This means that agglomerative hierarchical clustering doesn't scale well to large datasets. A future tutorial will talk more about this.
This Week’s Book
I was recently asked about using Generative AI to accelerate DIY data science work.
Not surprisingly, my response was that the first step is to build the requisite skills (otherwise, how would you recognize hallucinations?)
The second step is to learn how to prompt the LLM (e.g., ChatGPT) effectively:
This book offers an interesting take on engineering your LLM prompts. It will show you how to build and submit your prompts using Python code.
I see this as overkill, to be honest. However, the book also covers prompting strategies regardless of how you interact with the LLM (e.g., I use ChatGPT's web interface instead of Python code).
That's it for this week.
Stay tuned for next week's newsletter covering how distances are calculated in agglomerative hierarchical clustering.
Stay healthy and happy data sleuthing!
Dave Langer
Whenever you're ready, there are 4 ways I can help you:
1 - Are you new to data analysis? My Visual Analysis with Python online course will teach you the fundamentals you need - fast. No complex math required, and it works with Python in Excel!
2 - Cluster Analysis with Python: Most of the world's data is unlabeled and can't be used for predictive models. This is where my self-paced online course teaches you how to extract insights from your unlabeled data.
3 - Introduction to Machine Learning: This self-paced online course teaches you how to build predictive models like regression trees and the mighty random forest using Python. Offered in partnership with TDWI, use code LANGER to save 20% off.
4 - Is machine learning right for your business, but don't know where to start? Check out my Machine Learning Accelerator.